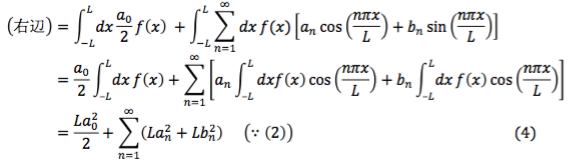パーセバル の 等 式 例題
夏目 アラタ の 結婚 結末パーセバルの等式 | 日々の日記 - 理系ノート. パーセバルの等式. 2019.07.25. [mathjax] 目次. パーセバルの等式とは. f (x) f (x) のフーリエ級数の係数に関して、以下がパーセバルの等式です。 displaystylefrac {1} {pi}displaystyleint_ {-pi}^ {pi} {f (x)}^2 dx=displaystylefrac {a_ {0}^2} {2}+displaystylesum_ {n=1}^ {infty} (a_ {n}^2+b_ {n}^2) π1 ∫ −ππ f (x)2dx = 2a02 + n=1∑∞ (an2 + bn2) ただし. 
きくや 酒店 チラシ関数 f (x) f ( x) の −π < x < π − π < x < π における複素フーリエ級数展開は f (x) = ∞ ∑ n=−∞cneinx f ( x) = ∑ n = − ∞ ∞ c n e i n x ここでは正負別々に極限をとるのではなく,同じペースで極限をとります.つまり f (x) = lim N →∞ N ∑ n=−N cneinx f ( x) = lim N → ∞ ∑ n = − N N c n e i n x ということです.. 9. フーリエ変換の性質(3): パーセバルの等式 ― 正規直交展開と . 9. フーリエ変換の性質 (3): パーセバルの等式 ― 正規直交展開としてのフーリエ変換. 9. 1 パーセバルの等式. やらない夫. フーリエ変換の性質の3つめだ.パーセバルの等式とかパーセバルの関係とか呼ばれるものを紹介しよう.. やる夫. 聞いたことあるお.たぶん数学の授業でやったお.. やらない夫. ついでに,これと等価なんだが「一般化パーセバルの等式」などと呼ばれるものも紹介しておこう.. やる夫. んーと,例えば式 ( 9.5 )で な場合が式 ( 9.1 )に一致するので,確かにある種の一般化になっているわけだお.…ってあれ? 今「等価」って言ったかお? やらない夫. ああ.言った.. やる夫. 等価と一般化じゃだいぶ話が違うお.そもそも本当に等価なのかお?. Parsevalの等式を使ったいくつかの問題 | てっぃちMarshの数学 . Parsevalの等式は以下のような式になる。 1/(2π)∫[-π→π]|f(x)|²dx=Σ[-∞→∞]|c[k]|² ここで、f(x)が複素関数ならば、|f(x)|²は、f(x)とその複素共役な関数 bar-f(x)の積である。 c[k]もそれが複素数ならば、|c[k]|²は、c[k]と複素共役 bar-c[k. ベッセルの不等式・パーセバルの等式とは:有限のケースで . 1. どうも、木村( @kimu3_slime )です。 フーリエ解析や関数解析では、ベッセルの不等式やパーセバルの等式と呼ばれるものが登場します。 今回は、それを線形代数の枠組み、有限のケースについて紹介し、証明します。 目次 [ 非表示] ベッセルの不等式. いびき か か なくなっ た
白木 位牌 と はパーセバルの等式. こちらもおすすめ. 特別 養護 老人 ホーム はなぞの
マクドナルド 裁判で敗訴ベッセルの不等式 は、次のような不等式です。 V V を(有限次元の) 内積空間 、 a_1,dots,a_n a1,…,an を 正規直交 なベクトルの集まりとする(必ずしも基底でなくて良い)。 任意の x in V x ∈ V に対して、. PDF 例題11 - shibaura-it.ac.jp. 例題 区間 [ ; ] 上の f(x) = x のフーリエ級数に対するパーセバルの等式を使っ て以下の級数の値を手順 (1)-(5) に従って求めよ。 k2. k=1. 以下の直交関数系の線形結合のうち、関数 f(x) に最も近いものを求めよ。 近 さの尺度としては、講義で説明した、 y 座標の差の 2 乗を区間 [ ; ] におい て積分したもの ( の半分 ) を用いよ。 ; cos x; sin x; cos 2x; sin 2x; : : : ; cos nx; sin nx. g. 関数 f(x) の区間 [ ; ] におけるフーリエ級数を示せ。 (上記 (1) で求めた線 形結合の n を大きくしたときの極限が関数 f(x) の区間 [ ; ] におけるフー リエ級数である。 ). パーセバルの定理 - 数学についていろいろ解説するブログ. パーセバルの定理とは、もとの関数のフーリエ級数と、積分の間に成り立つ等式のことである。 2018年8月7日追記:以下の記事も参照. 数学についていろいろ解説するブログ. id:shakayami. 三角関数の直交性とフーリエ級数. 概要 を上で定義された連続関数とする。 この関数を三角関数の無限和で表すことができた場合、以下のような形になるはずだ。 $$f (x)=frac {a_0} {2}+sum_ {n=1}^ {infty}left [a_ncos { (nx)}+b_nsin { (nx)}right]$$ ここでなぜをで割っているかについては、読み進めればわかるとだけ言っておこう。 問題はこれらの係数が、具… 2018-08-07 23:00. 6. フーリエ級数:特性 とパーセバル等式. フーリエ級数:特性とパーセバル等式. 計測システム研究室章忠. フーリエ級数の復習. 5.1 周期2Lの場合. n n . 任意の区分的に連続の関数f(t) に関して、有限の長さ2L(L>0)を切り出して、周期の周期関数として扱うことができる。 注意:関数f(t) のフーリエ級数は関数の奇偶性に関係する. 5.2.1 偶関数と奇関数のフーリエ級数. 5.2.2. 余弦と正弦展開. 同じ関数でも異なるフーリエ級数で表現できる。 5.3.2 複素フーリエ級数. 公式: cos. nx. einx. inx. 2. , sin. nx. einx . inx. 2 i. 1. ( x )~ c einx c. n. c einx. n. 【フーリエ解析】その12:パーシバルの等式(フーリエ変換版 . 今回は、フーリエ変換に対するパーシバルの等式です。 ほとんど同じですが、和が積分に変わっているので注意深く見てください。. 第13回: 【フーリエ級数とパーセバルの等式】関数を波で . 【2020年度東北大学工学部】毎週月曜日リアルタイムオンライン配信2021年度第3セメスター月曜日13:00-応用数学AのYouTube Live配信です。第14回は . 【第十九章】フーリエ変換でのパーシヴァルの等式【数学 . 【フーリエ解析】ww.youtube.com/watch?v=VY4IkqgJiVA&list=PLvJgUfWjlUOVrAhN25RDf9YGhe9ocqbPHフーリエ解析第十九章、フーリエ変換での . PDF フーリエ解析の基礎と応用 問および演習問題の解答. 倉田 和浩. 2020年11月12日改訂. 目 次. 第1章 複素数,オイラーの公式1. 第2章 関数項級数の収束4. 第3章 フーリエ級数の例8. 第4章L2最良近似とベッセル不等式15. 第5章 ディリクレ核と各点収束定理21. 第6章 ポアソン核とパーセバルの等式27. 第7章 有界区間上の熱方程式31. 第8章 有界区間上の波動方程式36. 第9章 フーリエ変換41. 第10章 フーリエ変換の反転公式46. 
アコム 会社 に バレ た第16章 ポアソンの和公式72. 付章A演習問題と解答77. パーセヴァルの等式 - Wikiwand. 数学の解析学の分野において、マルク=アントワーヌ・パーセバルの名にちなむパーセヴァルの等式 は、函数のフーリエ級数の総和可能性に関する基本的な結果である。 幾何学的には、内積空間に対するピタゴラスの定理と見なされる。. PDF 解析II演習 (B622) mail([email protected]. 例題-9-2.[フーリエ級数展開] 次の関数をフーリエ級数展開せよ. (1) f(x) = x3 − x (2) f(x) = x2 (3) f(x) = x2 − x 例題-9-3.[パーセバルの等式] (1) 例題9-1-(1)とパーセバルの等式を用いて、 ∑∞ n=1 1 n2 = ˇ2 6 であることを示せ. (2) 例題9 ∑. 4.6 Parseval の等式 - 明治大学. 4. 6 Parseval の等式. 4. 6. Parseval の等式. Next: 4.7 完全正規直交系の存在 Up: 4. 内積空間、Hilbert 空間 Previous: 4.5 Bessel の不等式. 桂田 祐史. 2017-04-30. ベッセルの不等式とその詳しい証明 | 数学の景色. 発展~パーセバルの等式~ 関連する記事. ベッセルの不等式とその詳しい証明. 以下で,{ e_n}が正規直交系(orthonormal system)であるとは,langle e_n,e_mrangle = begin{cases} 1 & n=m, 0 & nne m end{cases}すなわち,互いに直交する大きさ 1のベクトルの集まりということです(→正規直交系・正規直交基底)。 定理1(ベッセルの不等式; Bessels inequality) Xを内積空間,{e_n}_{n=1}^inftysubset Xを正規直交系とする。 このとき,任意の xin Xに対して,. PDF 最適化の数理. 2 1. 線形計画問題 生産計画問題を例として,線形計画問題とはどういった問題なのか見ていこう.また,そ の解決法の1 つである線形計画法についても確認していく. 1.1 線形計画問題の例 例題 1.1 ある会社では,原料Ⅰ, Ⅱ, Ⅲを使って,2 種類の製品 #, $を生産している.製品 #. フーリエ変換例題集【なんとなく学ぶフーリエ解析】 - 「なんとなくわかる」大学の数学・物理・情報. 大学の数学や物理を「分かりやすく、簡潔にまとめた」サイトがあればいいなと思い、作ってみることにしました。 自分も勉強中の身ですので、もしかしたら間違っていることを書いているかもしれません。なので、参考程度に見てください(笑)。. PDF 『スタンダード工学系のフーリエ解析・ラプラス変換』第1刷正誤表 7.3 標本化信号からの原信号の復元 7.3 標本化信号からの原信号の復元. 例題6.4 の詳細な解法は例題5.2 ですでに解説済みなので,43 ページを参 照されたい. 展開 問題 6.1 以下の式で表される時間関数に対する積分を,パーセバルの等 式を用いて解け.すなわち (f t)=AF( 2 sin( πF t) (πFt)) 2 に対する | ∞ -∞ (f t . フーリエ変換の意味と応用例 | 高校数学の美しい物語. フーリエ変換とは. フーリエ級数展開 とは,周期関数を三角関数(or 複素指数関数)の和で表すというものでした(→ フーリエ級数展開の公式と意味 , 複素数型のフーリエ級数展開とその導出 )。. 具体的には,周期 2 k pi 2kπ の関数 f (x) f (x) で適切な . パーシバルの定理の証明とパワースペクトルについて. パーシバルの定理は、元の信号とそのフーリエ変換との間に成り立つ性質を示しており、時間軸でのエネルギーと周波数軸でのエネルギーとが等価であることを述べている。これからパワースペクトルの概念や自己相関係数の性質をみて、ウィーナーヒンチンの定理を導出する。. パーセバルの恒等式 - 数式で独楽する. 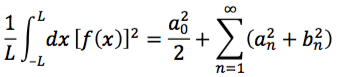
鬼 の 手形 岩H^s の空間に属する関数は,ある程度の「滑らかさ」をもっており, s は滑らかさを表すある種の指標になっています。この空間では,ある種の「微分」を考えることができるようになり, 微分方程式の解を求めるのにも活用されます。 ヒルベルト空間の性質. 応用数学(塩田)2021年度 - Kochi U. 応用数学(塩田)2021年度. パーセバルの等式. フーリエ展開から級数和を求める道具として有名なのがパーセバルの等式です。. Th.14 周期 2π 2 π を持つ関数 f (x) f ( x) が連続、かつ、区分的になめらかであるとする。. 庭 で バーベキュー 違法
鼻 の 皮 が 剥けるそのフーリエ展開可能を (♯) ( ♯) と . うさぎでもわかる信号処理・制御工学 第12羽 離散時間フーリエ変換(Dtft) | 工業大学生ももやまのうさぎ塾. そこで、離散的な関数 ( f(n) ) に対してもフーリエ変換を計算できるように式の形を書き換える必要があります。 (2) 連続フーリエ変換から離散時間フーリエ変換へ. 積分というのは、下の図のように細かく刻んだ長方形の面積の和を計算する演算でしたね。. フーリエ変換の諸性質 - Emanの物理数学. そういうわけで, (10) 式は今使っている流儀の場合だけで成り立つ公式であることに気を付けよう. さて, 上の式で としたなら, 次の式が成り立つはずだ. これはこれまでも出てきている「 パーセバルの等式 」のフーリエ変換の場合における形である. 補足 - パーセバルの等式 - Coocan. 自己相関はパワースペクトルを逆フーリエ変換して求められる【Wiener-Khintchineの定理】. t=0とおくと、エネルギーがx (t)とX (ω)で表わされる【Parsevalの等式】. よく使われる上記の3つの式を示す。. 皇 學 館 大学 落ち た
保育園 担任 の 先生 へ の お礼 の 手紙 例文1番目の式は次のように計算できる。. 2番目の式は次のよう . フーリエ解析の基礎と応用 - 株式会社サイエンス社 株式会社新世社 株式会社数理工学社. 第11章 フーリエ変換に対するパーセバルの等式 11.1 パーセバルの等式(良い関数に対して) 11.2 パーセバルの等式(一般の関数に対して) 演習問題 第12章 r上の熱方程式 12.1 熱方程式の初期値問題 12.2 最大値原理と解の一意性. ベッセルの不等式・パーセバルの等式. sin関数や cos 関数の部分はノルム2乗としてπが出てきた・・・と見ることができます。 すると,パーセバルの式は 「f(x)のノルムの2乗」 = 「各基底関数のノルムの2乗の総和」 という式として見ることができます。 これは3次元ベクトルで言うところの3平方 . 複素フーリエ級数を分かりやすく解説!【なんとなく学ぶフーリエ解析】 - 「なんとなくわかる」大学の数学・物理・情報. この式は複素数の概念を使っているので、普通の関数と区別して「複素関数」と言います。. とりあえず今はこの公式が成り立つものだとして話を進めていきましょう。 このオイラーの公式を使うと、先ほどのフーリエ級数を次の図のような「 複素フーリエ級数 」に変形することが出来ます。. 【材料力学】はりのたわみ計算方法・例題で解説 | カワハラ雑記. 例題の計算. 例題の画像には縦弾性係数がすでに書かれていますが、材質は軟鋼のss400なので、縦弾性係数は206,000 mpaとなります。 たわみの計算. 断面二次モーメントやたわみの係数など、計算に必要なパラメータが揃ったので、いよいよ大詰めです。. f(x) = xcos(x) [-π:π]のフーリエ級数展開 | ばたぱら. まとめ. 奇関数なので、フーリエ係数を求める計算は苦労しないだろう。. f (x)=sin^2 (x) [0:π]のフーリエ正弦級数・余弦級数. f (x)= |sin (x)| [-π:π]のフーリエ級数展開. 奇関数のフーリエ級数展開の例題である。. 積分の計算は丁寧にやっておきたい。. 6項までで . フーリエ解析の基礎と応用 倉田 和浩(著/文) - 数理工学社 | 版元ドットコム. 理工系の学生を対象にフーリエ解析の基本的事項から偏微分方程式の解法など応用例まで解説.例題や演習問題を適宜掲載し分かり易く丁寧にまとめられた好個の教科・参考書となっている. - 引用:版元ドットコム. フーリエ変換まであと一歩!フーリエの積分公式 | Imaginary Dive!!. フーリエの積分公式. フーリエ級数展開は a0 /2 + a1 ⋅ cosx + a2 ⋅ cos2x+ . と離散的な数値の無限和(級数)で周期関数を表します. 一方, 特別な操作を行うと, 無限級数( ∑ )は積分( ∫ )に変換でき, 積分にすると離散的な値ではなく, 連続した値の和と . PDF 1.5 フーリエ級数展開とパーシバルの等式. 1.5 フーリエ級数展開とパーシバルの等式 問. 関数f(x)を周期2π の周期関数とする。以下の各問に答えよ。 (1) 関数f(x) = jxj (¡π • x < π)のフーリエ級数展開は f(x) = π 2 ¡ 4 π ∑1 n=1 1 (2n¡1)2 cos(2n¡1)x である。これにパーシバルの等式を適用して ∑1 n=1 1 (2n¡1)4 . バーゼル問題 | 日々の日記 - 理系ノート. バーゼル問題とは (displaystylesum_{k=1}^{infty} displaystylefrac{1}{k^2}=displaystylefrac{pi^2}{6}) という等式で、オイラーが解いた。. 必ず解いておきたい!恒等式問題3選・詳しい解説付き|高校生向け受験応援メディア「受験のミカタ」. 今回は恒等式の問題を扱います。. 比較係数法、数値代入法、応用問題の3つのパターンをご用意しました!. もちろん詳しい解説付きです。. ぜひこの3パターンの問題で、恒等式の基礎を攻略しましょう♪. 武神 姫 ぶ じん き アマテラス
急 に 思い出す スピリチュアル※恒等式の基礎や計算方法についてまだ理解が不 . ベクトルのノルム | ユークリッド空間 | ユークリッド空間 | 数学 | ワイズ. 次元空間 の要素であるベクトル が与えられたとき、それに対して、 と定義される実数 を の ノルム (norm)と呼びます。. ベクトル を任意に選んだとき、その任意の成分 は実数であるため は非負の実数です。. さらに は加法と乗法について閉じていること . リプシッツ条件と微分方程式の解の一意性 | 高校数学の美しい物語. 大雑把に言うと「出力の変動が,入力の変動の定数倍でおさえられる」という条件です。詳しくは後述します。 微分方程式の初期値問題 を考えるときに重要な条件です。 リプシッツ条件を満たせば,微分方程式の解が一意に定まるので嬉しいです。. パーセバルの定理 - Wikiwand. パーセバルの定理 とは、フーリエ変換がユニタリであるという結果を一般に指す。大まかに言えば、関数の平方の総和(あるいは積分)が、そのフーリエ変換の平方の総和(あるいは積分)と等しいということである。フランスの数学者マルク=アントワーヌ・パーシバルの1799年の級数に . PDF スペクトル解析基礎 - 東京大学. 1 連続時間のスペクトル 1.1 スペクトルの導入 1.1.1 パワースペクトル ある定常確率過程x(t) の信号に対し,フーリエ変換を X(!) = Z 1 1 dt x(t)e i!t (1.1) で定義する.周波数f = !=2ˇ を用いるならば x~(f) = Z 1 1 dt x(t)e 2ˇift (1.2) である.区別のために,! が引数のときは大文字にして,f が引数のときは . 【フーリエ変換】計算式の原理・意味 | 西住工房. フーリエ変換で周波数成分を解析する例. 次のような周期的な入力信号 を用意します。 (1) ここで周波数 [Hz], Noiseは雑音とします。 をフーリエ変換で周波数領域に変換すると になります。 から振幅スペクトル を計算し、グラフ化すると以下のようになります。. 右が入力信号 、左が振幅 . ヘヴィサイド関数の積分表示について (フーリエ変換との関連) | Math Relish. ヘヴィサイド関数の積分表示について (フーリエ変換との関連) ヘヴィサイド関数 は定義が非常に単純であるが故に,原点での特異性がしばしば議論から覆い隠されるか,超関数的な観点の議論でも導関数としてディラックのデルタ関数を与える程度の言及 . 開水路の等流計算(流量を求める) | 科学技術計算ツール. 河川や水路などの開水路で、水深や流速が場所により変化しない流れを等流といいます。このページでは、Manning(マニング)公式を用いた等流の計算を行ないます。ここでは、水深と勾配から流量、フルード数を計算します。. PDF 中村伝『統計力学』. 中村伝『統計力学』. 本稿は統計力学の教科書 中村伝,1997,統計力学物理テキストシリーズ10,株式会社岩波書店,東京 を,要点と途中計算の分離した見通しの良い自己完結的テキストへと再構成し,さらに補足・考察を加えた ノートである.ただし本稿 . PDF フーリエ級数の性質. フーリエ級数の性質. フーリエ級数の性質. 山本昌志∗. 2006年12月18日. 概要 フーリエ級数の不連続点での値,項別微分と積分を学習する.さらに,パーセバルの等式と誤差の関 係も学習する.. 1 前回の復習と本日の内容. 本日の内容は,教科書[1]のp.231-236 . フーリエ変換の大事な性質〜線形性・シフト・畳込み・微分〜 | もろみ先輩の日常. シフトの定理は変換前の時間領域での遅延が,周波数領域では位相のシフトになっていることを表しています。 これは様々な場面で利用しますので是非覚えて下さい。 畳み込み定理. 畳み込みに対する性質ですが,先に畳み込みという概念を説明します。. 直交関数系 - Emanの物理数学. このような性質を持つ関数の集まりを「 直交関数系 」と呼ぶことにしよう. 互いに直交する多数のベクトルどうしの内積を取ったときの状況に良く似ているからだ. 「関数系」という言葉は「関数の集まり」くらいの意味で使っている. 沖縄 本島 と 宮古島
レンチキュラー 印刷 と はまた (3) 式の左辺の . PDF 離散フーリエ変換 - Kanazawa U. 本章では,さらに周波数領域における標本化を考え,時間領域と周波数領域の双方で標本化された信号のフーリエ変換(Discrete Fourie Transform: DFT)とその性質,畳み込み和,及びフィルタリング等について述べる。. ディジタル計算機における信号の数値表現が必然的 . 正規直交系・正規直交基底 | 数学の景色. 正規直交系とは,大きさが1であり,互いに直交するベクトルの集まりを指します。また,正規直交基底(完全正規直交系)とは,正規直交系で,かつ全てのベクトルがそれらを用いて表現可能なことをいいます。正規直交系・正規直交基底について,定義と具体例を見ていきましょう。. パーセバルの定理とウィーナー・ヒンチンの定理 | Excel VBA 数学教室. パーセバルの定理ある関数 $f(t)$ のフーリエ変換をとします。このとき $mid f(t)mid^2$ の全変域にわたる積分はとなります . 2 パーセバルの等式. 2. パーセバルの等式. のようにフーリエ級数で表すことができる.式 ( 4 )の両辺に を乗じて 2 ,関数が定 義されている区間で積分を行う 3 .. が得られる.これを パーセバルの等式 と言う.直交関数系のピタゴラスの定理のよ うなものである.フーリエ . 4.5 Bessel の不等式 - 明治大学. 4. 5 Bessel の不等式. とする。. 任意の に対して、 は の への直交射影である。. ゆえにピタゴラスの定理から、 ゆえに 左辺はピタゴラスの定理より であるから、 これが任意の について成り立つことから、. 内積空間 において、正規直交系 と が与えられた . マルク=アントワーヌ・パーセバル - Wikipedia. 1799年の2つ目の論文では、現在パーセバルの定理として知られる定理について述べているが、証明は行っていない(自明であると主張している)。 パーセバルは1801年の論文でこの定理をさらに発展させ、さまざまな 微分方程式 を解くのに用いた。. うさぎでもわかる信号処理・制御工学 第11羽 フーリエ変換 | 工業大学生ももやまのうさぎ塾. 理系大学生が確実に習うフーリエ変換について、導出方法を丁寧に記述し、さらに実際の期末試験での解き方を例題や練習問題などで分かりやすく記載しました。 . 1つの式から、フーリエ変換、フーリエ逆変換の2つの公式を導出できるのは不思議ですね . 技術計算製作所:フーリエ級数展開 ==機械設計に必要な情報とWebアプリ、ソフトウエアを公開しています-/science/math/fourier-. 特に等式条件が成り立つとき、 パーセバルの等式 と呼びます。.